Introduction

  • Learned representations are utilized in various downstream applications.
  • Today these represntations are rigid
    • we are forced to use the same high dimensional embedding vector across multiple tasks.
    • different tasks might have different resource/accuracy constraints.
  • At the same time, deep learning models today tend to diffuse information across the entire vector.
    • Not honouring the coarse-to-fine granularity of human perception.
  • Current methods to solve this problem:
    • Training multiple low dimensional models.
    • Jointly optimize subnetworks of varying capacity.
    • post-hoc compression.
  • Issues with these methods:
    • Training/Maintenance overhead.
    • Numerous expensive forward passes.
    • Significant drop in accuracy.
  • Matryoshka Represenation Learning (MRL) learns representation of various capacities within same high dimensional vector.

Implementation

  • Following implementation is for fully supervised representation learning via multi class classification.

  • For \(d \ \epsilon \ N\), consider a set \(M \subset [d]\) of representation sizes.

  • For a datapoint \(x\) in the input domain \(X\), our goal is to learn a d-dimensional representation vector \(z \ \epsilon \ R^d\).

  • For every \(m \ \epsilon \ M\), MRL enables each of the first m dimensions of embedding vector, \(z_{1:m} \ \epsilon \ R^m\) to be independently capable of being a transferrable and general purpose representation of the data point.

  • Usually \(M\) consists of halving until representation size hits a low dimenstional bottleneck.

  • Suppose we are given a labelled dataset: \(D= \{(x_1,y_1),...,(x_N,y_N)\) where \(x_i \ \epsilon \ X\) is an input point and \(y_i \ \epsilon \ [L]\) is the corresponding label.

  • MRL optimizes the following mult-class classification loss:

    \({_{\{W^{(m)}\}_{m \ \epsilon \ M }, \theta_F}}^{min} \frac{1}{N} \sum_{i \ \epsilon \ [N]}\sum_{m \ \epsilon \ M}c_m. L(W^{(m)}.F(x_i;\theta_F)_{1:m};y_i)\) where

    • \(L: R^L \times [L] \mapsto R_+\) is the multi-class softmax cross-entropy loss function.
      • can be solved using sub-gradient descent methods.
    • \(W^{(m)} \ \epsilon \ R^{L \times m}\) is a linear classifier
    • \(F(.;\theta_F): X \mapsto R^d\) is the neural network.
    • \(\theta_F\) is used to parametrize learnable weights of the neural network.
    • \((c_m \ge 0)_{m \ \epsilon \ M}\) is for relative importance of losses (all set to 1).

  • Can be made efficient through weight tying: \(W^{(m)} = W_{1:m}\)

    • Known as Efficient Matryoshka Representation Learning (MRL-E).

    Applications

    Classification

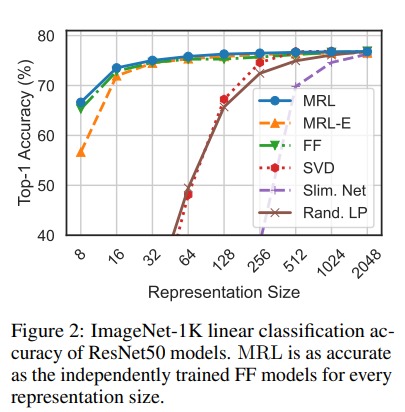
    linear-classification-accuracy

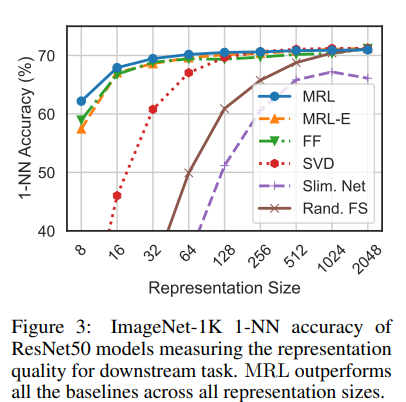
    1-nn-accuracy

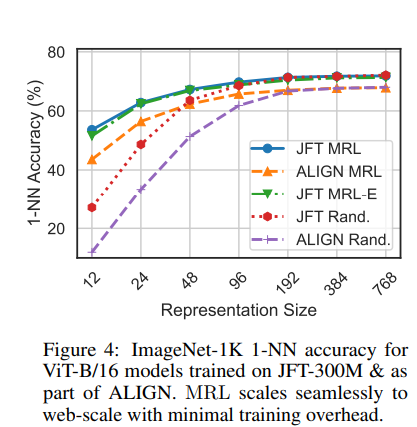
    1-nn-accuracy-VitB

Adaptive Classification

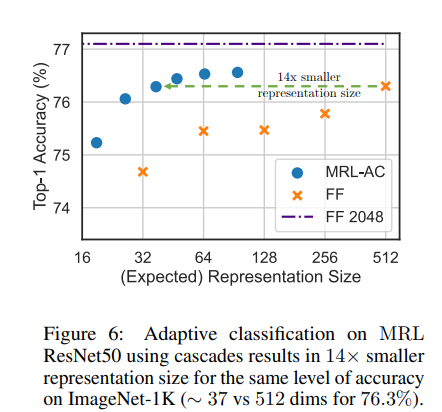
  • Coarse to fine granularity of the representation allows model cascades for Adaptive Classification.
  • Learn thresholds on max softmax probability for each nested classfifier on a holdout validation set.

  • Use these thresholds to decide when to transition to higher dimensional representation.

    adaptive-classification

Retrieval

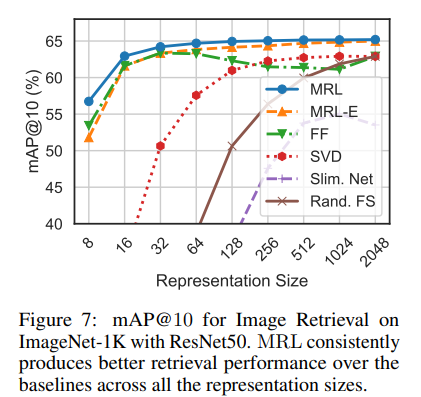
map retrieval

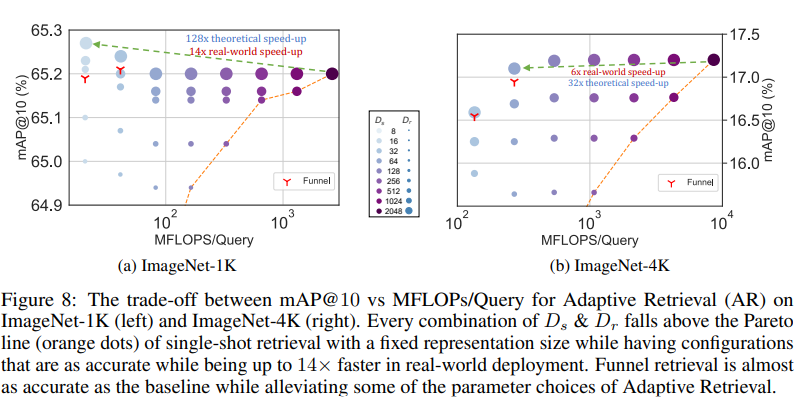
Adaptive Rretrieval

  • For a given query, shortlist K docs using lower dimensional representation, \(D_r\).
  • Followed by re-ranking with higher capacity representation, \(D_s\).
  • Funnel Retrieval:
    • Thins out initial shortlist by repeated re-ranking and shortlisting with a series of increasing capacity representation.

adaptive retrieval