RoFormer: Enhanced Transformer with Rotary Position Embedding

Introduction

• Existing approaches to the relative position embedding based on adding position encoding to context representation.
• Current work, introduces Rotary Position Embedding (RoPE).
  • leverages positional information into learning process of Pretained Language Models.
• RoPE decays with relative distance increased.
  • desired for natural language encoding.
• Achieves better performance in long text benchmarks compared to alternatives.

Related Work

Preliminary

• let \(S_N=\{w_i\}_{i=1}^N\) be a sequence of \(N\) input tokesns with \(w_i\) being the \(i^{th}\) element.

• The corresponding word embedding is denoted as: \(E_N=\{x_i\}_{i=1}^N\) where \(x_i \in R^d\) is the d-dimensional word embedding of token \(w_i\) without position information.

• The self-attention first incorporates position information to the word embeddings and transforms them into queries, keys and value representations.

\[q_m=f_q(x_m,m), k_n=f_k(x_n,n), v_n=f_v(x_n,n) \ (1)\]

where \(q_m,k_n,v_n\) incorporate the \(m^{th}\) and \(n^{th}\) positions through \(f_q, f_k \ and \ f_v\) respectively.

• query and key are then used to compute attention weights and output is computed as weighted sum over the value:

\[a_{m,n} = \frac{\exp(\frac{(q_m^{T}k_n)}{\sqrt{d}}}{\sum_{j=1}^N\exp(\frac{(q_m^{T}k_j)}{\sqrt{d}}}\] \[o_m = \sum_{n=1}^Na_{m,n}v_n\]

• Existing approaches for transformer based position encoding focus on choosing a suitable function to form equation (1).

Absolute Position Embedding

• Typical choice of eq. (1)

\(f_{t:t \in \{q,k,v\}}(x_i, i) = W_{t:t\in \{q,k,v\}}(x_i + p_i)\) where \(p_i\) is a d-dimensional vector depending on position of token \(x_i\).

• Two types:

  • Use a set of trainable vectors. \(p_i\in\{p_t\}_{t=1}^L\) where \(L\) is maximum sequecne length.

  • Use sinusoidal function: \(p_{i, 2t} = \sin(i/10000^{2t/d})\) \(p_{i, 2t+1} = \cos(i/10000^{2t /d})\)

    • Each dimension of the positional encoding corresponds to a sinusoid
    • The wavelengths form a geometric progression from \(2\pi\)to \(10000 \times2\pi\)
    • For any fixed offset k, \(p_{i+k}\)can be represented as a linear function of \(p_i\).
    • Current proposal related to this intuition.

Relative Position Encoding

• Shw et.al. [2018]

  \(f_q(x_m) = W_qx_m\) \(f_k(x_n,n)=W_k(x_n+\tilde{p_r^k})\) \(f_v(x_n,n)=W_v(x_n+\tilde{p_r^v})\)

  where \(\tilde{p_r^k},\tilde{p_r^v} \in \R^d\) are trainable position embeddings.

  • \(r=clip(m-n, r_{min}, r_{max})\) represents relative distance.

• Dai et al. [2019]

  \[q_m^Tk_n = x^T_mW^T_qW_kx_n + x^T_mW^T_qW_kp_n + p^T_mW^T_qW_kx_n + p^T_mW^T_qW_kp_n\]
  • Replace absolute position embedding \(p_n\) with its sinusoidal-encoded relative counterpart \(\tilde{p}_{m-n}\)
  • Replace absolute position \(p_m\)in third and fourth term with two trainable vectors independent of the query positions.
  • \(W_k\) distinguished for content-based and locatin based vectors.

  • Position information in the value term is removed.

    \[q_m^Tk_n = x^T_mW^T_qW_kx_n + x^T_mW^T_q\tilde{W_k}\tilde{p}_{m-n} + u^TW^T_qW_kx_n + v^TW^T_q\tilde{W_k}\tilde{p}_{m-n}\]

• He et al. [2020]

  \[q_m^Tk_n = x^T_mW^T_qW_kx_n + x^T_mW^T_qW_k\tilde{p}_{m-n} + \tilde{p}_{m-n}^TW^T_qW_kx_n\]

• These methods directly add position information to context repesentation.

Proposed Approach

Formulation

• We require inner product of query \(q_m\) and key \(k_n\) to be formulated by a function \(g\), which takes as input only word embeddings \(x_m,x_n\) and their relative position \(m-n\).

\[<f_q(x_m,m),f_k(x_n,n)>=g(x_m,x_n,m-n)\]

Rotary Position Embedding

2D Case

• Solution : Use geometric properties of vectors in 2-d and their complex forms(Express other terms also as complex numbers for the equations to make sense).

\(f_q(x_m,m)=(W_qx_m)e^{im\theta}\) \(f_k(x_n,n)=(W_kx_n)e^{in\theta}\) \(g(x_m,x_n,m-n)=Re[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}]\)

where \(Re[.]\) is the real part of complex number and \((W_kx_n)^*\) is conjugate complex of \((W_kx_n)\), \(\theta\in R\) is a preset non-zero constant.

• In multiplication form:

\[f_{\{q,k\}(x_m,m)}= \begin{pmatrix} cosm\theta & -sinm\theta\\ sinm\theta & cosm\theta \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)}\\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix}\]

General form

• To generalize the results to any \(x_i\in R^d\) where \(d\) is even, we divide the d-dimension space into \(d/2\) subspaces and combine them:

\[f_{\{q,k\}}(x_m,m)=R^d_{\Theta,m}W_{\{q,k\}x_m}\] \[R^d_{\Theta,m}= \begin{pmatrix} cosm\theta_1 & -sinm\theta_1 & 0 & 0 & \cdots & 0 & 0\\ sinm\theta_1 & cosm\theta_1 & 0 & 0 & \cdots & 0 & 0\\ 0 & 0 & cosm\theta_2 & -sinm\theta_2 & \cdots & 0 & 0\\ 0 & 0 & sinm\theta_2 & cosm\theta_2 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & cosm\theta_{d/2} & -sinm\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & sinm\theta_{d/2} & cosm\theta_{d/2} \\ \end{pmatrix}\]

is the rotary matrix with pre-defined params \(\Theta=\{\theta_i=10000^{-2(i-1)/d}, i \in [1,2,...,d/2]\}\)

• Applying to self-attention equation:

\[q_m^Tk_n=(R^d_{\Theta,m}W_qx_m)^T(R^d_{\Theta,n}W_kx_n)=x^TW_qR^d_{\Theta,n-m}W_kx_n\]

Properties of Rope

• Long Term Decay
• Computational efficient expression (because of sparsity):

\[R^d_{\Theta,m}x= \begin{pmatrix} x1\\ x2\\ x3\\ x4\\ \vdots\\ x_{d-1}\\ x_d\\ \end{pmatrix} \otimes \begin{pmatrix} cosm\theta_1\\ cosm\theta_1\\ cosm\theta_2\\ cosm\theta_2\\ \vdots\\ cosm\theta_{d/2}\\ cosm\theta_{d/2}\\ \end{pmatrix} + \begin{pmatrix} -x1\\ x2\\ -x3\\ x4\\ \vdots\\ -x_{d-1}\\ x_d\\ \end{pmatrix} \otimes \begin{pmatrix} sinm\theta_1\\ sinm\theta_1\\ sinm\theta_2\\ sinm\theta_2\\ \vdots\\ sinm\theta_{d/2}\\ sinm\theta_{d/2}\\ \end{pmatrix}\]

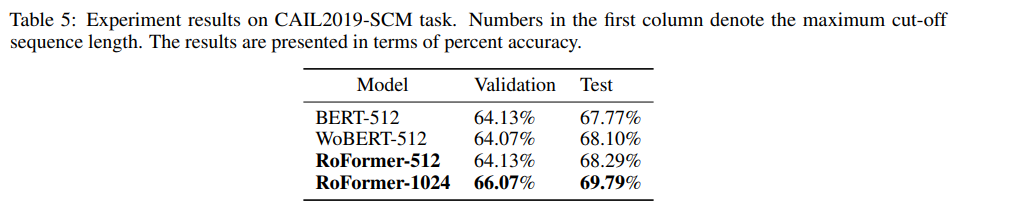
Evaluation

Machine Translation

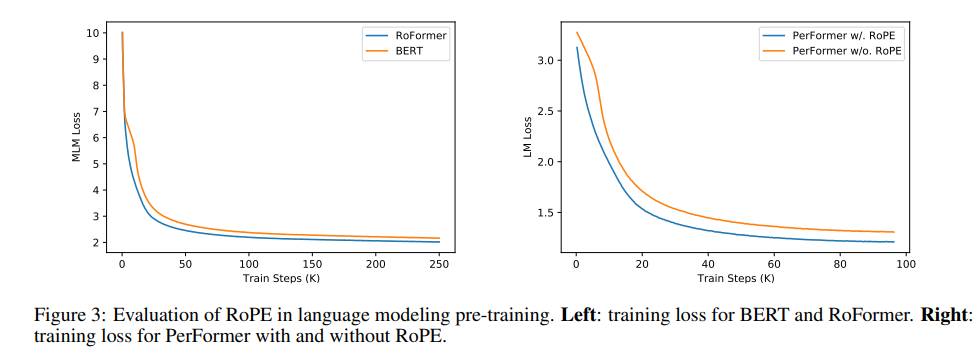
Pre-training Language Modeling

Fine-tuning on GLUE tasks

Evaluation on Chinese Data